数据结构 排序
数据结构-排序
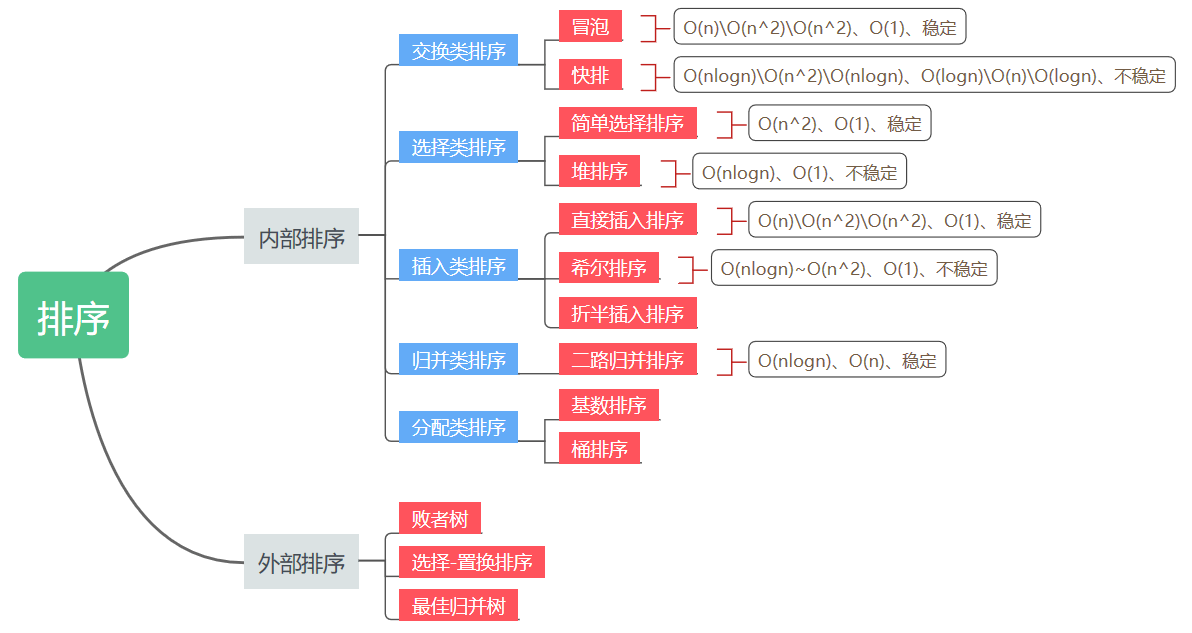
排序算法分类:
-
交换类排序
每一趟排序都通过,一系列的交换动作,让一个记录排到它最终的位置上
- 冒泡排序
- 快速排序
-
选择类排序
每一趟排序都选出一个最值,并把它和序列中第一个或最后一个记录交换,这样最值就记录到位了
- 简单选择排序
- 堆排序
-
插入类排序
在一个已经有序的序列中,插入一个新的记录,从而包含这个新纪录的整体也是有序的
- 直接插入排序
- 希尔排序
- 折半插入排序
-
归并排序
将两个或两个以上的有序序列合并成一个新的有序序列
-
基数排序
时间复杂度比较
O(1) < O(logn) < O(n) < nO(logn) < O(n^2) < O(n^3) < O(2^n)
1.1 冒泡排序
- Java代码
public static void bubleSort(int [] array) {
for (int i = 0; i < array.length - 1; ++i) { // 排序趟数
// boolean swapped = false;
for (int j = 0 ; j < array.length - 1 - i; ++j) { // 每一趟排序多少次
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
// swapped = true;
}
}
//if (!swapped) {
// break;
//}
}
}
-
时间复杂度
- 最坏情况下(待排列长度为n的数据为逆序)
外层循环执行,n-1趟
内层循环执行,n-1-i,期中0<=i<n-1
所以总共的排序次数为:(n-1- 0) + (n-1 -1) + … + (n-1 -(n-2)) = (n-1)*(3n-4)/2
时间复杂度为O(n^2)
- 最好情况(待排列长度为n的数据为顺序)
内层循环执行一遍后,发现相邻两个元素都不需要交换,可以直接break外层循环,一共遍历了(n-1- 0)次,时间复杂度为O(n)
- 平均复杂度
O(n^2)
-
空间复杂度
如果有一个额外的temp变量,在交换的时候用于记录,则是O(1)
-
稳定性
稳定
1.2 快速排序
- Java代码
public static void quickSort(int [] array, int left, int right) {
if (left > right) {
return;
}
int leftPointer = left;
int rightPointer = right;
int base = array[leftPointer]; // 定义基准元素
while(leftPointer < rightPointer) { // 只要左指针和右指针没有指向统一元素就继续交换
while (leftPointer < rightPointer && array[rightPointer] >= base) { // 从右往左寻找第一个小于基准的元素
--rightPointer;
}
array[leftPointer] = array[rightPointer]; // 把比基准小的元素放到低端
while (leftPointer < rightPointer && array[leftPointer] <= base) { //从左往右寻找第一个大于基准的元素
++leftPointer;
}
array[rightPointer] = array[leftPointer]; // 把比基准大的元素放到高端
}
array[leftPointer] = base; // 把基准元素放到,这个该放的位置
// 对左边进行快排
quickSort(array, left, leftPointer - 1);
// 对右边进行快排
quickSort(array, leftPointer+1, right);
}
-
时间复杂度
- 最坏情况(待排序的序列为正序或者逆序 )
每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,它就是一棵斜树。此时需要执行n‐1次递归调用,且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录,也就是枢轴的位置,因此比较次数为
(n-1)+(n-2)+…+1 = (n-1)*n/2,所以时间复杂度为O(n^2)
- 最好情况(Partition每次都划分得很均匀 )
Partition每次都划分得很均匀,如果排序n个关键字,其递归树的深度为logn
仅需递归logn次 。需要时间为T(n)的话,第一次Partiation应该是需要对整个数组扫描一遍,做n次比较。然后,获得的枢轴将数组一分为二,那么各自还需要T(n/2)的时间 ,也就是T(n)≤2T(n/2) +n
于是,有以下不等式推断:
T(n)≤2T(n/2) + n, T(1)=0
T(n)≤2 (2T(n/4)+n/2)+ n= 4T(n/4)+2n ,把T(n/2)通过T(n)=2T(n/2)展开
T(n)≤4 (2T(n/8)+n/4)+2n=8T(n/8)+3n
……
T(n)≤nT (1)+(logn)×n= O(nlogn)
所以时间复杂度为 O(nlogn)
- 平均复杂度
O(nlogn)
-
空间复杂度
就空间复杂度来说,主要是递归造成的栈空间的使用,最好情况,递归树的深度为logn,其空间复杂度也就为O(logn),最坏情况,需要进行n‐1递归调用,其空间复杂度为O(n),平均情况,空间复杂度也为O(logn)
-
稳定性
不稳定
1.3 简单(直接)选择排序
每一步都是在无序的记录中找到最小值,并与无序记录的第一数交换,最终所有数据有序
-
Java代码
public void selectSort(int[] a) { for (int i = 0; i < a.length; i++) { int index = i; for (int j = i + 1; j < a.length; j++) { if (a[j] < a[index]) { index = j; } } //交换两个数 if (index != i) { int temp = a[i]; a[i] = a[index]; a[index] = temp; } } } -
时间复杂度
由代码中的两层循环可以看出,两层循环的执行次数和初始序列没有关系。外层循环总会执行n次,内层循环总会执行n-1次。
所以,最好情况=最坏情况=平均复杂度,即O(n^2)
-
空间复杂度
O(1)
-
稳定性
不稳定
1.4 堆排序
- Java代码
import java.util.Arrays;
/**
* HeapSort
*
* @author Flynn
* @version 1.0
* @description TODO
* @email liufenglin@163.com
* @date 2019/3/24
*/
public class HeapSort {
public static void main(String[] args) {
int [] a = {100, 3 ,8, 10, -12, -500, 0, 0, 1,1};
heapSort(a);
System.out.println(Arrays.toString(a));
}
static void heapSort(int []a) {
//初始建堆
buildMaxHeap(a,a.length);
// 循环进行堆调整和交换,堆的大小从n到2
for(int i = a.length-1;i > 0;i--) {
// 交换
a[i] = a[0] ^ a[i];
a[0] = a[0] ^ a[i];
a[i] = a[0] ^ a[i];
maxHeapfy(a,0,i);
}
}
static void buildMaxHeap(int []a,int heapSize) {
for(int i = (heapSize-1 -1)/2; i >= 0 ;i--) {
maxHeapfy(a,i,heapSize);
}
}
/**
* 对二叉树中的指定节点进行,大根堆化
*
* @param a
* @param i
* @param heapSize
*/
static void maxHeapfy(int []a,int i,int heapSize) {
//数组a,第i个结点,heapSize是数组中实际要排序的元素的长度
int leftChild = leftChild(i);
//有的时候能够递归到叶子结点,叶子结点无后继,下面两个if都注意到了这一点
int rightChild = rightChild(i);
int largest = i;
if(leftChild < heapSize && a[leftChild] > a[largest]) {
largest = leftChild;
}
if(rightChild < heapSize && a[rightChild] > a[largest]) {
largest = rightChild;
}
if(largest != i) {
//把最大值给父结点
a[largest] = a[largest] ^ a[i];
a[i] = a[largest] ^ a[i];
a[largest] = a[largest] ^ a[i];
//发生交换之后还要保证大根堆性质
maxHeapfy(a,largest,heapSize);
}
}
static int parent(int index) {
return (index - 1)/2;
}
static int leftChild(int index) {
//左孩子
return 2*index + 1;
}
static int rightChild(int index) {
//右孩子
return 2*index + 2;
}
}
-
时间复杂度
-
建堆时间复杂度分析,一个高度为h的节点,maxHeapfy的复杂度为O(h)。经过计算,初始化建堆过程时间:O(n)
-
更改堆元素后重建堆时间,循环n -1次,每次都是从根节点往下maxHeapfy,所以每一次时间是 logn(一个高度为h的节点,maxHeapfy的复杂度为O(h)),总时间:(n-1)logn = nlogn - logn ;
所以时间复杂度为O(n) + O(nlogn - logn) = O(nlogn)
- 最好情况=最坏情况=平均复杂度
因为堆是一种完全二叉树,它具有平衡二叉树的性质,堆总是平衡的,所以时间复杂度不会出现变化
-
-
空间复杂度
如果有一个额外的temp变量,在交换的时候用于记录,则是O(1)
-
稳定性
不稳定
1.5 归并排序
归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
-
Java代码
public static void mergeSort(int [] a, int p, int r) { if (p >= r) { // p >= r 表示该子数组最多有一个元素,所以已经排序好了 return; } int q = (p + r) / 2; mergeSort(a, p, q); mergeSort(a, q+1, r); merge(a, p, q, r); } /** * 数组a,p、q、r是数组下标,且p<=q<r * a[p..q]和a[q+1..r]都是已经排好序的子数组 * 最后合并好后的排序数组是a[p..r] */ public static void merge(int [] a, int p, int q, int r) { int n1 = q - p + 1; // 计算子数组1的长度 int n2 = r - (q + 1) + 1; // 计算子数组2的长度 int [] L = new int[n1+1]; // 创建左数组,多出的1位用来设置哨兵,哨兵用来表示分组中数字已经分完,防止数组越界 int [] R = new int[n2+1]; // 创建右数组,多出的1位也用来设置哨兵 L[n1] = Integer.MAX_VALUE; // L哨兵大于R组中的任意数字 R[n2] = Integer.MAX_VALUE; // R哨兵大于L组中的任意数字,两个哨兵可以统一设置为无穷大 // 把数组a[p..q]复制到L[0, n1-1]; for (int i = 0; i < n1; ++i) { L[i] = a[p + i]; } // 把数组a[q+1..r]复制到R[0, n2-1]; for (int i = 0; i < n2; ++i) { R[i] = a[q + 1 + i]; } // 循环合并,一共需要合并r-p+1个数据,控制好循环次数防止哨兵添加到a数组(这会导致数组a的越界问题) for (int k = p, i =0, j = 0; k <= r; ++k) { if (L[i] <= R[j]) { a[k] = L[i]; i++; } else { a[k] = R[j]; j++; } } } /** * 如果没有设置哨兵,for循环可以改写如下 */ // for (int k = p, i = 0, j = 0; k <= r; ++k) { // if (i < n1 && j < n2) { // if (L[i] <= R[j]) { // a[k] = L[i]; // i++; // } else { // a[k] = R[j]; // j++; // } // } else if (i < n1) { // a[k] = L[i]; // i++; // } else if (j < n2) { // a[k] = R[j]; // j++; // } // } public static void main(String[] args) { int [] a = {1, 100, 70, 99, 1000, 56, 0}; mergeSort(a, 0, a.length-1); System.out.println(Arrays.toString(a)); } -
时间复杂度
因为归并过程形成的递归树是平衡的,所以时间复杂度不会出现变化。
O(nlogn)
算法导论的分治法部分有分析
-
空间复杂度
因为归并排序,需要转存整个带排序列,所以空间复杂度是O(n)
-
稳定性
稳定
1.6 插入排序
通过对未排序的数据逐个插入到合适的位置而完成排序工作
- Java代码
public void insertionSort(int [] a) //插入排序
{
int temp = 0;
for (int i = 1; i < a.length; i++)
{
temp = a[i]; // 记录需要被插入的元素
int j = i - 1; // 用j来保存i-1,避免直接操纵i
while(j >= 0 && temp < a[j])
a[j+1]=a[j]; // 后面的i位置保存较大的数字
j--;
}
a[j+1] = temp;
}
}
-
时间复杂度
-
最坏情况(被排序的序列是逆序的)
每一次外层循环,内层循环的次数都会执行最大次数,时间复杂度为O(n^2)
-
最好情况(被排序的序列是有序的)
内层循环始终不执行,只有外层循环执行。时间复杂度为O(n)
-
平均复杂度
O(n^2)
-
-
空间复杂度
有一个额外的temp变量,在交换的时候用于记录,是O(1)
-
稳定性
稳定
1.7 shell排序
希尔排序又叫缩小增量排序,将待排序的序列分为若干个子序列(以n/2为间距),然后分别对若干个子序列进行插入排序。然后再以n/4为间距,划分子序列,然后分别进行插入排序。重复上述过程,最后再以1为间距,即对整个序列进行插入排序
增量序列还可以选择9,5,3,2,1等。只要增量序列中,没有除1以外的公因子,且最后一个增量值为1即可。
-
Java代码
public void shellSort(int[] a) { for (int r = a.length / 2; r >= 1; r /= 2) { //划组排序 for (int i = r; i < a.length; i++) { // 循环内为插入排序的代码 int temp = a[i]; int j = i - r; while (j >= 0 && temp < a[j]) { a[j + r] = a[j]; j -= r; } a[j + r] = temp; } } } -
时间复杂度
分析十分复杂,和增量序列有关,一般是O(nlogn)~O(n^2)
-
空间复杂度
O(1)
-
稳定性
不稳定
总结
**堆排序**、**快速排序**、**希尔排序**、**简单(直接)选择排序**是不稳定的排序算法,而**基数排序**、**冒泡排序**、**直接插入排序**、**折半插入排序**、**归并排序**是稳定的排序算法。