数据结构 树
数据结构-各种二叉树
树形结构:树是一种非线性的结构。它是由若干个节点构成的集合,它有唯一的根和若干棵不相交的子树组成,其中每一颗子树又是树。
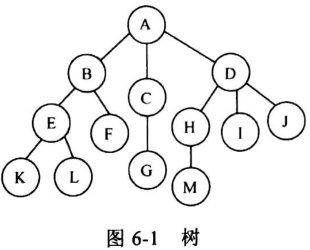
树的术语

树形结构分类
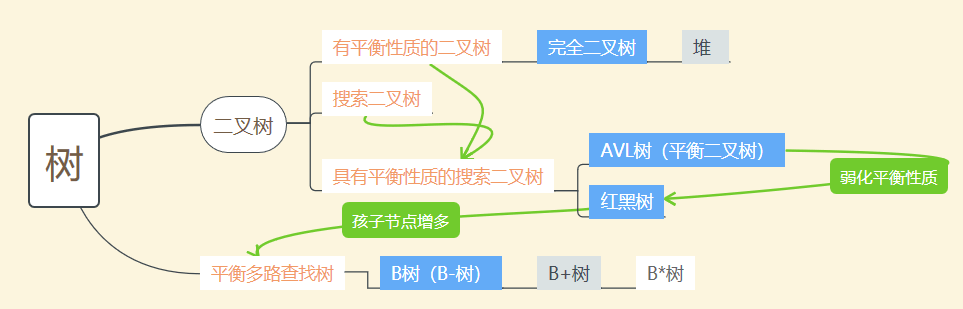
1.二叉树
二叉树是有以下两点限制的树:
(1)每个节点最多只有两颗子树;(2)子树有左右之分,不能颠倒
1.1 有平衡性质的二叉树
一棵二叉树中的任何一个节点,该节点的左右子树的高度差的绝对值不超过1
满二叉树 :除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树
- 完全二叉树(完全二叉树仅仅是一种结构,与值无关,节点之间没有大小关系)
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
https://www.cnblogs.com/myjavascript/articles/4092746.html
-
堆
堆就是满足一定性质(节点之间大小关系)的完全二叉树。
大根堆:任何一颗子树的最大值都是树的头部(父亲大于等于孩子) ;
小根堆:任何一颗子树的最小值都是树的头部(父亲小于等于孩子)
1.2 搜索二叉树
一棵二叉树中的任何一个节点,该节点的左子树的值比它小,右子树的值比它大
注:通常搜索二叉树不含有重复的信息(所以不可能存在等于的情况),如果有重复的信息,可以产生(key, ListValue)的结构来保存重复的值信息。
搜索二叉树的每个结点包括4个属性:key、left、right、parent
1.3 具有平衡性质的搜索二叉树
1.3.1 AVL树(就叫平衡二叉树)
AVL树适合用于插入删除次数比较少,但查找多的情况 。
不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的
1.3.2 红黑树
红黑树是一颗搜索二叉树,并具有一定的平衡性质(弱平衡),且它的每一个结点都增加一个存储来表示结点的颜色。红黑树可以保证在最坏的情况下基本动态集合操作的时间复杂度为O(logn)
红黑树=红黑性质+二叉搜索树
红黑树的每个结点包括5个属性:key、left、right、parent、color
相对于要求严格平衡的AVL树来说,红黑的旋转次数变少,所以对于搜索、插入、删除操作多的情况下,我们就用红黑树
-
红黑性质:
1.每个结点都是红色或黑色的 2.根节点是黑色的 3.每个叶结点(NULL结点)是黑色的 4.如果一个结点是红色的,则它的两个子节点都是黑色的 5. 从一个结点出发到该结点的所有后代叶结点的简单路径上,均包含相同数目的黑色结点
【这个性质确保了红黑树的弱平衡性质:对任何一条从根到叶子的简单路径上,确保没有一条路径会比其它路径长出2倍】 -
红黑树的基本操作
- 旋转-左旋
- 旋转-右旋
- 插入
- 删除
1.4 平衡多路查找树
1.4.1 B树(又称B-树)
B树是一种平衡多路查找树
- 一颗m阶B树的性质
| 1.每个结点至多有m棵子树 |
|---|
| 2.除根节点外,其它每个分支结点至少有 m/2向上取整 棵子树 |
| 3.根结点至少有两颗子树(除非B树只包含一个结点) |
| 4.所有叶结点在同一层 |
1.4.2 B+树
1.4.3 B*树
1.5 其它
- 哈夫曼树(最优二叉树)