Kmp算法

2019, May 29    

KMP算法

[TOC]

1.应用场景

字符串匹配问题。

demo：现在有主串S、模式串P，判断模式串P是否是主串S的子串。如果是，找出P在S中第一次出现时的下标。

2.从暴力求解到KMP算法

2.1暴力求解

思路：从左到右一个个匹配，如果这个过程中有某个字符不匹配，将子串向右移动一位，继续从左到右一一匹配。

（0）主串的0号元素和模式串的0号元素匹配成功

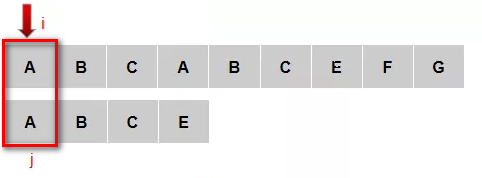
1568355630289

（1）主串的1号元素和模式串的1号元素匹配成功

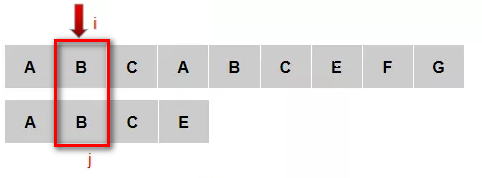
1568355745742

（2）主串的2号元素和模式串的2号元素匹配成功

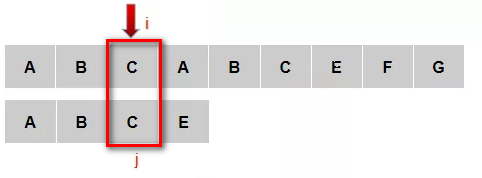
1568355794825

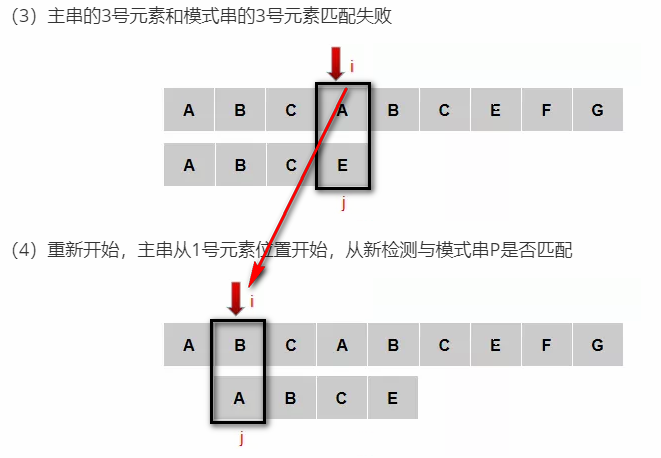
（3）主串的3号元素和模式串的3号元素匹配失败

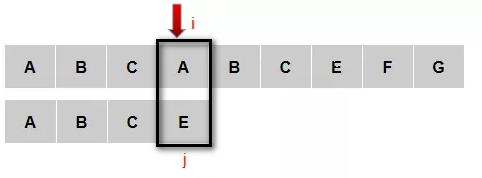
1568355858688

（4）重新开始，主串从1号元素位置开始，从新检测与模式串P是否匹配

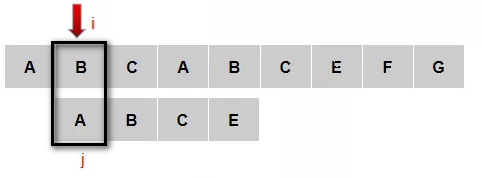
1568356093878

（5）重新开始，主串从2号元素位置开始，从新检测与模式串P是否匹配

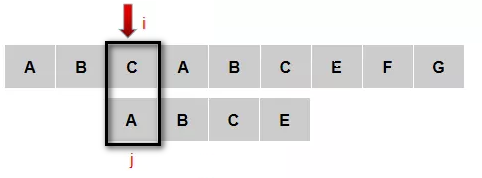
1568356251018

（6）重新开始，主串从3号元素位置开始，从新检测与模式串P是否匹配，主串从3号元素和模式串的0号元素匹配成功

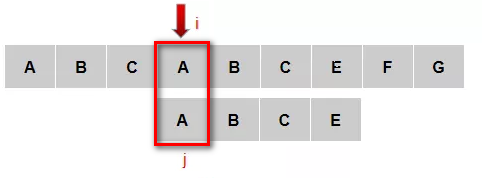
1568356314953

（7）主串从4号元素和模式串的1号元素匹配成功

1568356452998

（8）主串从4号元素和模式串的2号元素匹配成功

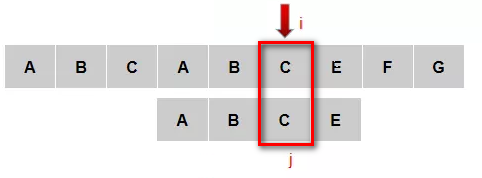
1568356496126

（9）主串从4号元素和模式串的3号元素匹配成功，确定模式串P是主串S的子串，P在S中，第一次出现的index=3

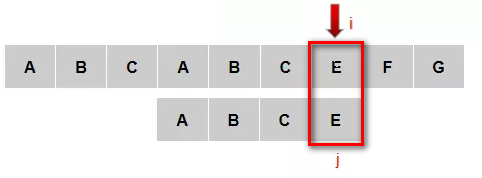
1568356522481

2.2KMP算法
暴力求解的存在的问题

1568357220441

当A和E不匹配后，模式串P后移一位（如下图所示），此时，模式串P的前三位（ABC）和主串的[1-3]（BCA）肯定是不匹配的，无需浪费这几次比较，最好是直接让i不变，j==0

1568356093878

KMP思路

在需要重新开始匹配的时候，利用前面匹配的信息，保持i指针不变，通过修改j指针，让子串尽量地移动到有效的位置。

比如：

1568356845313

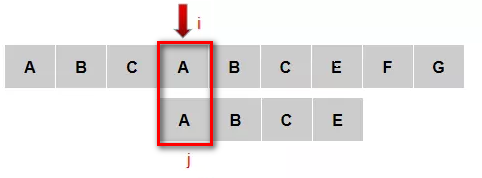
从第（3）步到第（4）步，能否保持i不变，依赖之前匹配的信息，通过把j移动到有效位置上，进行新的匹配

因此，整个KMP的重点就在于当某一个字符与主串不匹配时，我们应该知道j指针要移动到哪？

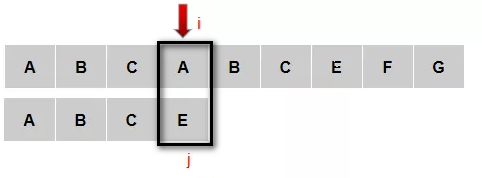
如下图：A和E不匹配了，我们要把j移动到哪？显然是第0位。为什么？因为前面有一个A相同可以用：

1568357220441

所有，移动j，再进行匹配，如下图

1568357319380

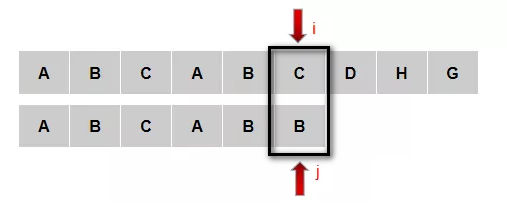
我们再来看另一种情况：如下图所示，C和B匹配失败，主串的AB[3,4]和模式串的AB[0,1]一致，所以i不动，j可以移动到2位置

1568431162558

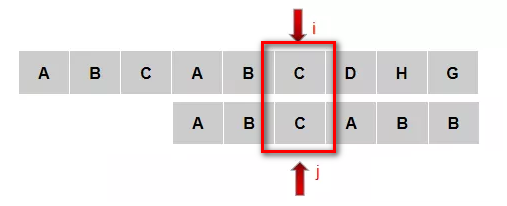
1568432269808

观察可知，**匹配失败的时候，j变为k,j前面的的n个字符等于子串开头到k位置的n个字符的值**

即：P[0 ~ k-1] == P[j-k ~ j-1]

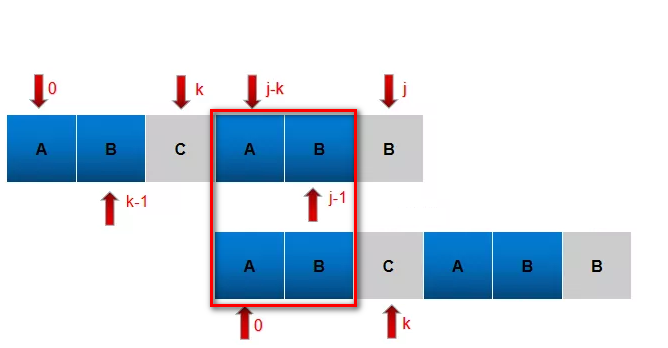
1568448765633

这时我们发现规律了，其实就是要求当前j之前的字符串，也就是ABCAB[0-j-1]它的首尾对称的长度最大长度，也就是PMT值。j向前移动n个字符的值=PMT值

PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。

前缀

指除了最后一个字符以外，一个字符串的全部头部组合；

后缀

指除了第一个字符以外，一个字符串的全部尾部组合；

例如：

对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀集合为{”ba”, ”a”}。
两个集合的交集为{”a”}，那么长度最长的元素字符串”a”的长度为1，
所以对于”aba”而言，它在PMT表中对应的值就是1。

对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 
两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”的长度为3。
所以对于”ababa”而言，它在PMT表中对应的值就是3。
求Next数组

接下来核心就是求得模式串P每个下标元素对应的k值即可，因为在P的每一个位置都可能发生不匹配，我们要计算每一个位置j对应的k，所以用一个数组next来保存，next[j] = k，表示当S[i] != P[j]时，j应该变为k。

求NEXT数组的代码

public class Next {

    public static int[] getNext(String ps) {
        char[] p = ps.toCharArray();
        int[] next = new int[p.length];
        next[0] = -1; // 
        int j = 0;
        int k = -1;
        while (j < p.length - 1) {
            if (k == -1 || p[j] == p[k]) {
                next[++j] = ++k;
            } else {
                k = next[k];
            }
        }
        return next;
    }
}

两种主要情况

if (k == -1 || p[j] == p[k]) {   第一种p[j] == p[k]
    next[++j] = ++k;
} else {                         第二种p[j] != p[k]
    k = next[k];
}

第一种p[j] == p[k]

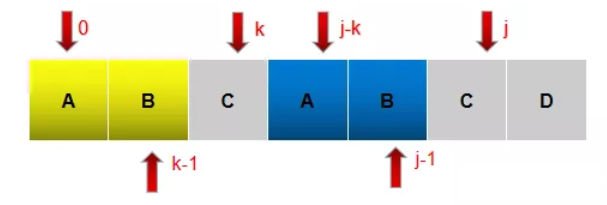
1568458791460

p[j] == p[k]时，有next[++j] = ++k;

第二种p[j] != p[k]

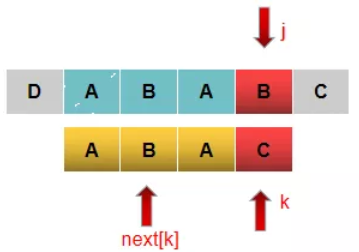
1568459079893

KMP代码
public class Kmp {
    public static int KMP(String ts, String ps) {
        char[] t = ts.toCharArray();
        char[] p = ps.toCharArray();
        int i = 0; // 主串的位置
        int j = 0; // 模式串的位置
        int[] next = getNext(ps);

        while (i < t.length && j < p.length) {
            if (j == -1 || t[i] == p[j]) { // 当j为-1时，要移动的是i，当然j也要归0
                i++;
                j++;
            } else {
                // i不需要回溯了
                // i = i - j + 1;
                j = next[j]; // j回到指定位置
            }
        }

        if (j == p.length) {
            return i - j;
        } else {
            return -1;
        }
    }
}
# Data Structure